Stackless Scala, Part 1: The Problem
Motivation
I am reading the paper, Stackless Scala with Free Monad, by Rúnar Bjarnason.
|
Also checkout Rúnar’s book Functional Programming in Scala. The book is excellent. |
In the paper, he illustrates a shortcoming if one were to write Scala in a functional style. I am a huge proponent of functional programming. Having been dabbling in Clojure, Haskell, and, now, Scala. Being able to write Scala in a functional way is very important to me. So, I am very interested in how the problem is solved in Scala. I believe the patterns introduced in the paper are being used by libraries like cats and scalaz.
Most importantly, these posts will serve as a study notes for myself. As a side effect, hopefully, these will be helpful to others as well.
Introduction
The example below is copied straight from the paper, and it is used to illustrate a shortcoming of writing functional style Scala. Let’s go over it.
The example given in the paper describes a function that zips every element of a list with its
index.
The zipIndex function will traverse the given list while maintaining some state.
The state being the index.
So if the list List(10, 20, 30) is passed into zipIndex,
the return value will be List((0,10), (1,20), (2,30))
where the first position of the tuples are the indices.
A State action is used to keep track of the state as well as the final return value.
The code for State and zipIndex is shown below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 case class State[S,+A](runS: S => (A, S)) { (1)
def map[B](f: A => B) = State[S,B](s => {
val (v, s1) = this.runS(s)
(f(v), s1)
})
def flatMap[B](f: A => State[S,B]): State[S,B] =
State[S,B](s => {
val (a, s1) = this.runS(s)
f(a) runS s1
})
}
def getState[S]: State[S,S] = State(s => (s, s))
def setState[S](s: S): State[S,Unit] =
State(_ => ((), s))
def pureState[S, A](a: A): State[S,A] = (1)
State(s => (a, s))
def zipIndex[V](as: List[V]): List[(Int, V)] =
as.foldLeft(pureState[Int, List[(Int,V)]](List())) (2)
((acc, v) => for {
xs <- acc
n <- getState[Int]
_ <- setState[Int](n + 1) (3)
} yield (n,v)::xs)
.runS(0)._1.reverse
| 1 | The State case class and pureState forms a monad. |
| 2 | Folding over the input list, where the return value of the fold is a State action. |
| 3 | Using for comprehension to calculate the next index,
and store it back to the State action. |
So far so good.
The implementation of zipIndex looks like a typical monadic computation
where different functions are composed together inside a monadic context.
We have a State action which contains a state and a value.
In this case, the state is the index we are going to assign,
and the value is the list of tuples.
Such implementation is fairly standard even in Haskell.
I have implemented the example in Haskell.
Here is zipIndex in Haskell.
1
2
3
4
5
6
7
8
9
10
11 zipIndex :: [a] -> ([(Int, a)], Int)
zipIndex xs = run (innerZipIndex xs) 0
where
innerZipIndex :: [a] -> MyState Int [(Int, a)]
innerZipIndex xs = foldM step [] xs
step :: [(Int, a)] -> a -> MyState Int [(Int, a)]
step acc e = do (1)
i <- getState
setState (i + 1)
return $ (i, e) : acc
| 1 | Get and update the state inside MyState monad. |
The Problem
There is, however, a major problem in the Scala implementation — it is not stack safe.
Meaning given a sufficiently large input list,
it will throw a StackOverflowError.
Let’s take a closer look at why it is overflowing the stack.
For that, I will focus on two functions,
zipIndex and the implementation of flatMap for State.
1
2
3
4
5
6
7
8
9
10
11
12
13
14 def flatMap[B](f: A => State[S,B]): State[S,B] =
State[S,B](s => {
val (a, s1) = this.runS(s)
f(a) runS s1
})
def zipIndex[V](as: List[V]): List[(Int, V)] =
as.foldLeft(pureState[Int, List[(Int,V)]](List()))
((acc, v) => for {
xs <- acc
n <- getState[Int]
_ <- setState[Int](n + 1)
} yield (n,v)::xs)
.runS(0)._1.reverse
Recall that, the Scala compiler will translation the for-comprehension into calls to flatMap.
Therefore, for every step of the fold in zipIndex,
it will call flatMap on the variable acc which is a State action.
Inside flatMap, a new instance of State will be created,
and the anonymous function being passed into that new instance of State will close over
the current instance of State (this line 3),
so that the runS method can be called.
Essentially, we are creating a nested stack of State actions as shown in the following screenshot.
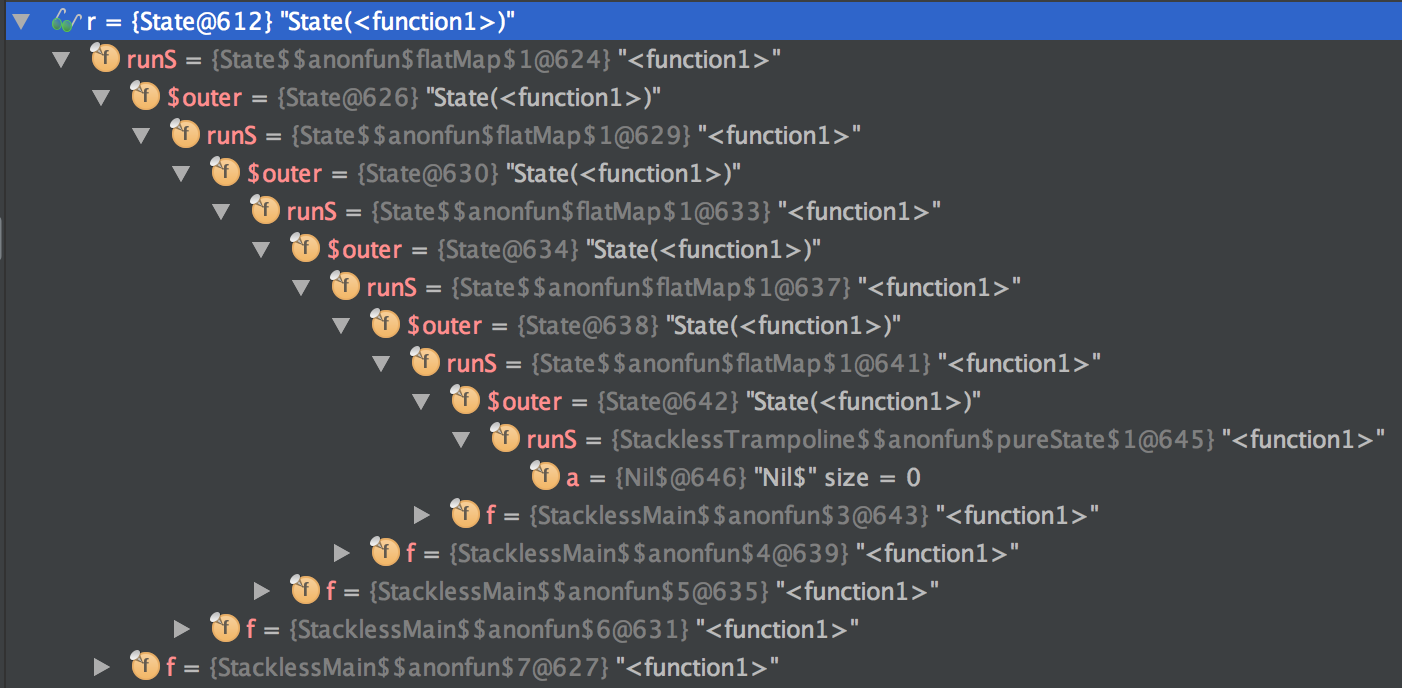
Going back to the zipIndex example, as we fold over the whole list,
we are creating a stack of State actions linear to the number of elements in the list.
So, when we evaluate the stack of State actions by calling runS,
before runS returns, it will call runS of its inner State action,
and that call to inner runS will call its inner State action’s runS and so on and so forth.
As the call goes deeper and deeper, it keeps creating new stack frames.
Eventually, there are more stack frames that the JVM can allow.
On my MBP, the zipIndex function will throw StackOverflowError
when the input is a list of around 4000 integers.
A list of about 4000 elements is not that big of an input,
such limitation makes functional programming in Scala not practical.
But fear not, there are solutions mentioned in the paper to the stack safety problem,
and I will talk about them in the subsequent posts.